Korona, etterspørsel og tilbud, og langsiktig vekst
Anvendt makroøkonomi, Campus Trondheim
Harding og Rattsø (2020), Mehlum og Torvik (2020)
Artikkelene på pensum er forholdsvis lett-lest, særlig Harding og Rattsø. For de som ikke rekker forelesning, så kan man finne noen bulletpoints her, mens man burde lese artikkelene for å få en god oversikt.
Det er verdt å nevne at begge artiklene er velformulerte samfunnsøkonomiske argumenter. Begge er gode eksempler på hva man kan sikte mot når du skriver en bacheloroppgave.
Koronakrisen og langsiktig vekstevne
Harding og Rattsø (2020)
Langsiktig ("strukturelle") problemer med norsk økonomi
Stagnasjon i realdisponibel inntekt
- Realdisponibel inntekt vokste med 300.000 per innbygger i 1990 til 614.000 per innbygger i 2008 - årlig vekst av 4%
- (Realdisponibel inntekt: BNP - kapitalslit + inntekt og overføringer fra utlandet, korrigert for inflasjon)
- Mellom 2008-2019 har realdisponibel inntekt falt med ca. 50.000kr. per innbygger.
- Realdisponibel inntekt fra SSB.
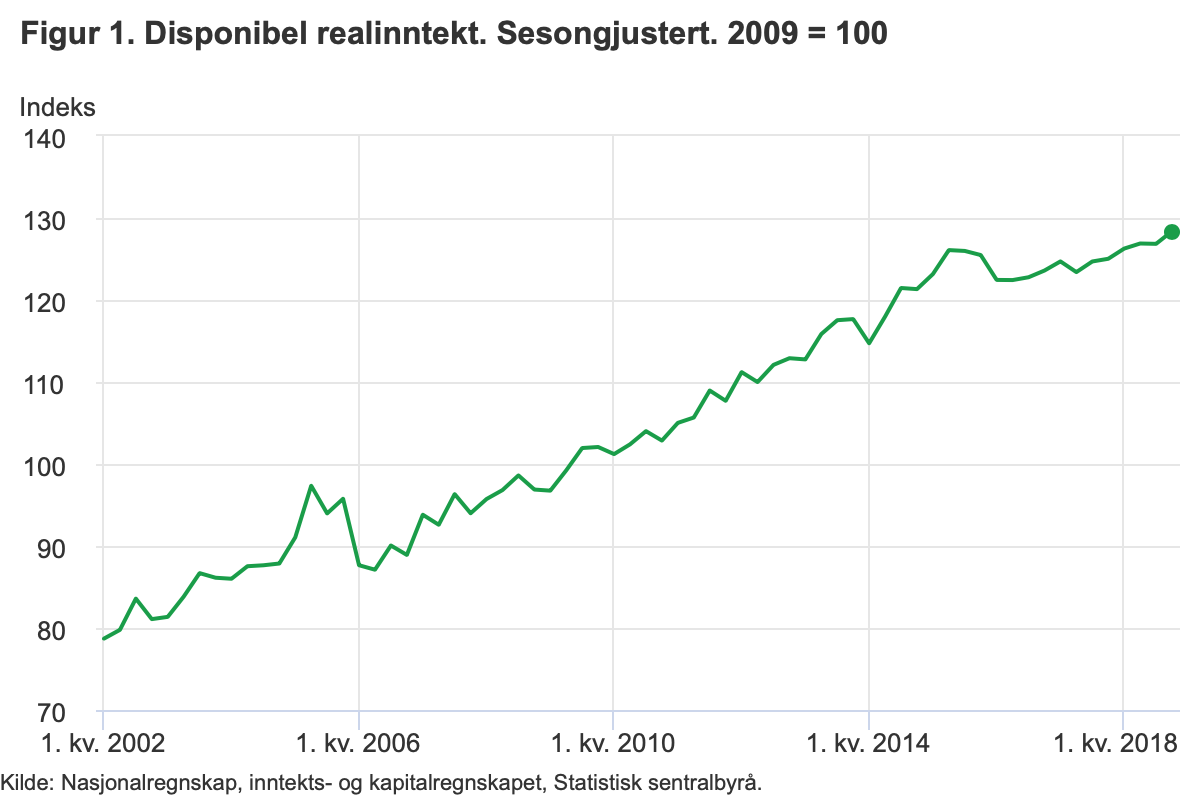
- Her er bruttonasjonalinntekt (inkluderer kapitalslit)
Økende finansieringsbehov for offentlig ressurrsbruk
- Flere offentlig ansatte
- Økt overføringer til "yrkespassive"
- Offentlig sektor: 25% av fastlandsøkonomien 1991-2006
- 28.4% i 2019
- Totale offentlige utgifter (ink investering) har økt fra 51,4% i 2007 til 58,4% i 2019
Fallende sysselsettingsandel
- "Har sunket siden 2008", men...
- Fallet størst blandt menn: 85-90%
- Andelen som mottar permanent stønader har økt
- Uføretrygd andel størst i OECD
- 14% i Norge
- 6% i Danmark og Sverige, OECD gjennomsnitt 6%
- 17% i gruppen 25-54% ikke sysselsatte.
- Uføretrygd blandt de unge 18-29 fordoblet seg 2000-2017
- Falt i samme perioder 50-66 åringer (pensjonsreform)
Lav produktivitetsvekst
Rask og handlekraftig
- Fokus på likviditet og dekking av tap
- utsettelse og reduksjon av skatter og avgifter
- lån hvor staten er garantist
- Inntektssikring for selvstendig næringsdrivende
- Full lønn for permitterte i en periode
- Reduksjon av arbeidsgiveransvar (15 til 2 dager)
Tilpasning til sterk interessegrupper
- NHO og LO presset for endring i permitteringsregler
- Bedriftene brukte endringene som anledning til å kvitte seg med ansatte.
- Mange som ikke lett kommer tilbake inn i arbeidslivet
Svak vekt på insentivmekanismer
Politikkrespons på krisen
Mer korporativt styre mellom politiske organer og interesseorganisjoner
- Burde være en tydelig fordeling og balanse mellom marked og stat.
- Markedsøkonomien burde være effektiv
- Staten må ha legitimetet
- Statlig innblanding kan svekke risikovurderinger og skape fornyelse.
- Kreativ destruksjon vs. zombiebedrifter
- Når staten dekker alle tap, så gir det feil signal om framtidig risiko - "Privateierskap vernet av staten istedenfor utfordret av markedet"
Økende politisk og økonomisk nasjonalisme
- Norsk økonomi er basert på utnyttelse av et globalt økonomi.
- Teknologisk utvikling viktigste faktor i langsiktig vekst - avhengig av å være åpen til verden.
Faremomenter for langsiktig vekst
Etterspørsel og tilbud i koronaens tid
Mehlum og Torvik (2020)
Vi kan trekke ut en rekke velutviklet begrep og modeller fra makroøkonomi for utviklingsland til å forklare det som skjer under korona.
-
Flaskehalser
- Noen nøkkelindustrier produserer ikke og kveler deler av økonomien
-
Rasjonering
- Kjøp av noen produkter må begrenses (utenom prismekanismen)
-
Tvungen sparing
- Når muligheten til å kjøpe varer begrenses, så kan husholdninger bli tvunget til å spare
- Dette kan føre til en ekstra bølge av etterspørsel ("pent up demand") når flaskehalsene blir borte.
-
Innsatsvarebegrenset produksjon
- Begrenset produksjon på grunn av mangel av innsatsvarer
-
Likviditetsbegrenset produksjon
- Begrenset produksjon på grunn av mangel på finansiering (selv for solide virksomhet)
-
sektorheterogenitet
- At ulike deler av økonomien blir påvirket på svært ulike måter
-
Kostnader som løper selv om produksjon stenger ned
- Bedrifter som må stenge pga korona har fortsatt kostnader som må betales.
En enkel modell
Vi begynner med en standard, enkel keynesian modell
Vi har produksjon = aggregert etterspørsel:
$$Y=C+I+G+NX$$Og en konsumfunksjon:
$$C=c(1-t)Y$$Som vi løser
$$Y= \frac{1}{1-c(1-t)}(I+G+NX)$$Denne enkle modellen har som hovedantakelse at produksjon blir bestemt av etterspørsel (Y=C+I+G+NX).
Men nedstengning av økonomien under Korona - dette innebærte at både tilbudet og etterspørselen forsvant for de nedstengte sektorene.
Vi trenger en modell som gir muligheten til å begrense tilbud i noen sektore og etterspørsel i andre.
En 2-sektor modell for finanspolitikk før korona.
\(Y_1\): Samlede produksjonen i de sektorene som må stenge ned
- Vi kan kalle dette for den utsattesektoren
\(Y_2\): Samlede produksjon i de sektorene som ikke må stenges
- Vi kan kalle dette for den kritiske sektoren
\(f\): andelen konsumentetterspørsel som retter seg mot sektor 1, \((1-f)\): andelen som retter seg mot sektor 2
Nå får vi:
$$Y_1 = fc(1-t)(Y_1+Y_2) + I_1 + G_1 + NX_1$$
$$Y_2 = (1-f)c(1-t)(Y_1+Y_2) + I_2 + G_2 + NX_2$$
Da kan vi løse for hver sektor
$$Y_1 = \frac{1}{1-fc(1-t)}(fc(1-t)Y_2+I_1+G_1+NX_1)$$
$$Y_2 = \frac{1}{1-(1-f)c(1-t)}((1-f)c(1-t)Y_1 + I_2+G_2+NX_2)$$
Når (i vanlige tider) produksjon er bestemt av etterspørsel, så får vi en samlet løsning der de to kurvene krysser hverandre.
$$Y=\frac{1}{1-c(1-t)}(I_1+I_2+G_1+G_2+NX_1+NX_2)$$
Med denne modellen kan vi se hva effekten er av finanspolitikk i vanlige tider.
Det man ser er at den samlet effekten på Y av å øke G er likt uansett om man øker G til den ene sektor eller den andre.
Med andre ord, om man retter finanspolitikken mot den utsatte sektoren (1) eller den kritiske sektoren (2) så vil det føre til samme samlet effekt (mens fordelingen blir annerledes)
En viktig poeng er at hvis vi øker vår stimulans til den kritiske sektoren (G2) så vil effekten på Y være via både den direkte effekten på Y2 men også indirekte effekten via Y1
En 2-sektor modell for finanspolitikk etter korona.
Nå modellerer vi en modell etter nedstengning.
Nå skal vi modellere at myndighetene har begrenset tilbudet fra sektor 1.
Nå er det sånt at både tilbudet og nødvendigvis etterspørselen er borte for sektor 1.
Vi kan skrive løsningen for sektor 2 under korona (\(Y_2^k\)) som:
$$Y_2^K = \frac{1}{1-(1-f)*c*(1-t)}*(I_2+G_2+NX_2) < Y^0_2$$
På grunn av avhengigheten mellom sektorene, så faller ikke bare produksjon i Y1, men også i Y2
Dette vil også føre til arbeidsledighet som er høyere også i Y2 sektor.
Finanspolitikk under korona
Vi kunne tenkt oss at vi kunne bare skifte etterspørselen fra sektor 1 til 2. Vi kan ikke spise på restaurant, så vi spiser mer hjemme. Men dette er problematisk:
- Det finnes ikke gode alternativer i sektor 2 for noen av varene i sektor 1
- Det er ikke nødvendig ledig kapasitet i sektor 1 for mye ekstra etterspørsel.
Resultatet blir derfor der en politikk som prøver å øke etterspørsel i sektor 2 for å gjøre opp for det som ble tapt i sektor 1 mislykkes. Man kan da heller ikke satse på å gjøre opp for den økte ledigheten i sektor 1.
Under korona, der utsattesektoren er nedstengt, vil effekten av finanspolitikk på Y være svakere enn før siden det er ingen indirekt effekt via Y1.
Hvor mye ekstra i stimulus - la oss si i form av en "lump-sum" kontantstøtte - måtte man bruke for å gjøre opp for bortfallet i sektoren?
Det måtte tilsvare hele den tapte produksjonen i første sektoren. Så hvis støtten er \(S^k\), og vi tar hensyn til at staten vil få noe av utgiften tilbake i skatter, så vil utgiften være:
$$(1-t)S^k$$Men hvis støtten kom i form av offtenlig kjøp og utgifter, så er størrelsen på den nødvendige utgiften:
$$(1-f)c(1-t)Y_1^0<(1-t)S^k$$Det vil si at offentlig kjøp er mer effektiv i å gjøre opp for bortfallet enn kontantstøtte. Hvorfor?
Fordi mye kontantstøtte forsvinner til sparing. Og den effekten blir enda sterkere, fordi nå er det sånt at mye av det folk ville brukt penger på før er nå borte. Det er ekstra mye sparing (tvunget sparing!)
Offentlig kjøp blir \(\frac{1}{(1-f)c}\) så effektiv som skattelette
Tilbudspolitikk i Korona
Tilbudspolitikk i korona har med å prøve å lette på uønsket flaskehalser mens man ikke letter på "ønsket" flaskehalser.
- Finansiering av likviditet for bedrifter
- Tiltak til næringer med mangel på innsatsvarer og sviktende etterspørsel (ikke direkt relatert til nedstengning)
- Faste kostnader som løper selv med nedstengning
Pengepolitikk i korona
I vanlige tider så tenker man på pengepolitikk som noe som vil øke etterspørselsen. Samtidig som det kan ha effekten av å øke prisnivået.
Vi viser det i en "AS-AD" (Aggregate Supply, Aggregate Demand) modell ved å skifte ut aggregert etterspørsel (Du kan trykke på Skift ut AD)
Men i koronatider kan vi også tenke at pengepolitikk gjør det lettere for bedrifter til å opprettholde likviditet, beholde sine ansatte, og få tak i råmaterialer.
Med andre ord så kan pengepolitikk også skifte ut tilbudskurven. Trykk på Skift ut AS for å se effekten.
Nå er effekten av pengepolitikk fortsatt ekspansiv, mens effekten på prisene er utydelig. Når etterspørsel skifter ut så presser det opp på priser, men når tilbud skiftes ut så er det dempende på priser.
En fallende tilbudskurv
En annen mulighet i kriseperioder er at tilbudskurven kan periodevis være fallende.
Det vises i figuren over. Ideen er at i krisetider så er det mange bedrifter som opplever likviditetsproblemer. Ekspansiv pengepolitikk som øker etterspørsel og forbedrer omsetning vil da ha effekten av å forbedre likviditeten i hele økonomien og gjøre det mulig for flere bedrifter til å produsere.
En annen tolkning er at mange bedrifter har høye løpende fastekostnader. Ved å øke omsetning, så får man også ned engangskostnaden og dermed kan bedrifter selge flere produkter til en lavere pris.
Oppgaver
Del 1: Harding og Rattsø
Her legger jeg ikke ut løsningsforslag siden man kan enkelt finne svar i artikkelen.
- Hva beskriver Harding og Rattsø som noen av de langsiktige probemer med norsk økonomi?
- Hva var regjeringens mål når de innførte krisepakkene i respons til koronapandemien
- Hva er faremomentene ved at interesseorganisasjoner får en sterk påvirkning på økonomisk politikk?
- Hva er faren for Norge av økende økonomisk nasjonalisme både hjemme og i utlandet?
Del II: Mehlum og Torvik
1.) La oss si vi har følgende to-sektor modell i likevekt:
$$Y_1 = \frac{1}{1-fc(1-t)}(fc(1-t)Y_2+I_1+G_1+NX_1)$$ $$Y_2 = \frac{1}{1-(1-f)c(1-t)}((1-f)c(1-t)Y_1 + I_2+G_2+NX_2)$$Der
-
$$c = 0,7$$
$$t=0,3$$
$$f=0,5$$
$$I_1 = 12$$
$$I_2 = 10$$
$$G_1 = 10$$
$$G_2 = 10$$
$$NX_1 = 0$$
$$NX_2 = 0$$
a. Hva er likevekts BNP i de to sektorene (\(Y_1\) og \(Y_2\) ) (I vanlige tider)?
b. Hvis man øker G1 med 5, hva er effekten på totalt BNP (\(Y=Y_1 + Y_2\))
c. Hvis man øker G2 med 5, hva er effekten på totalt BNP (\(Y=Y_1 + Y_2\))
d. Nå går vi ut i fra at pandemien har skjedd og produksjon i sektor 1 er stengt: \(Y_1 = 0\), Hva blir produksjon i sektor 2, \(Y_2^K\)?
e. Si at regjeringen vurderer å enten bruke kontantstøtte eller å bruke offentlig forbruk til å erstatte den tapte produksjonsen i sektor 1. Hvor mye måtte regjeringen bruke i kontantstøtte for å kompensere for den tapte BNP i sektor 2. Hvor mye måtte regjerningen bruke i offentlig forbruk for å erstatte den tapte produksjonen i sektor 2?
a.) Vi begynner med likevektsbetingelsen i sektor 1
$$Y_1 = \frac{1}{1-fc(1-t)}(fc(1-t)Y_2+I_1+G_1+NX_1)$$Og vi regner ut at
$$fc(1-t) = 0,5*0,7*0,7 = 0,245$$Og siden \(f=0,5\) så blir:
$$(1-f)c(1-t) = 0,5*0,7*0,7=0,245$$Da kan vi skrive likevektsbetingelsen som
$$Y_1 = 1,32[0,245Y_2 + 22]$$ $$Y_1 = 0,32Y_2 + 29$$På samme måte kan vi sette inn verdiene for Y_2:
$$Y_2 = \frac{1}{1-(1-f)c(1-t)}((1-f)c(1-t)Y_1 + I_2+G_2+NX_2)$$ $$Y_2 = 1,32[0,245Y_1 + 20]$$ $$Y_2 = 0,32Y_1 + 26,4$$Med to ligninger og to ukjente, så kan vi finne svarene:
$$Y_1^* \approx 42$$ $$Y_2^* \approx 40$$Og
$$Y^* = Y_1^* + Y_2^* = 82$$b.) Vi begynner med vår likevektsligninger:
$$Y_1 = 1,32[0,245Y_2 + G_1 + I_1]$$ $$Y_2 = 1,32[0,245Y_1 + G_1 + I_1]$$Så ser vi at:
$$\Delta Y_1 = 1,32[0,245 \Delta Y_2 + \Delta G_1]$$ $$\Delta Y_1 = 0,32 \Delta Y_2 + 6,6$$og
$$\Delta Y_2 = 1,32[0,245 \Delta Y_1]$$ $$\Delta Y_2 = 0,32 \Delta Y_1$$Med to ligninger og to ukjente får vi:
$$\Delta Y_1 = 7,3$$og
$$\Delta Y_2 = 2,34$$\Delta Y \approx 9,6
c.) Du burde kunne vise at man får samme resultat som i b.)
d.) Nå at sektor 1 er stengt ned med 0 i produksjon, så har vi bare en likevekt i sektor 2:
$$Y_2^K = 1,32[I_2 + G_2 + NX_2]$$ $$Y_2^K = 26,4$$e.)
Vi ønsker å beregne hvor mye økning i offentlig forbruk (G) eller kontantstøtte (S) vi trenger for å få produksjon i sektor 2 tilbake til hvor den var. Her skal vi anta at det ikke er mulig til å erstatte produksjonen som vi tapte i sektor 1 med økt produksjon i sektor 2.
Forskjellen i produksjon i sektor 2 var:
$$\Delta Y_2 = 40-26,4 = 13,6$$Hvis vi begynner med økt offentlig forbruk, så kan vi skrive:
$$13,6 = 1,32 \Delta G$$ $$\Delta G = 10,3$$Kontantstøtte vil påvirke BNP via konsumfunksjonen - økt inntekt vil føre til høyere konsum. Men da må vi ta høyde for konsumtilbøyeligheten - at bare andelen, c, av den nye inntekten vil gå til konsum:
$$13,6 = 1,32*cS$$ $$13,6 = 1,32*0,7S$$ $$S = 14,7$$Derfor trenger vi 14,7 i kontantstøtte for oppnå samme resultat som 10,3 i økt offentlig forbruk. Hvis målet er å øke BNP, så er offentlig forbruk en mer effektiv verktøy.
Men det er fortsatt gode grunner for å vurdere kontantstøtte. Kontantstøtte kan være mer målrettet til utsatte grupper - lavlønnet eller de som har mistet jobben. Hvis målet er å sikre at alle har nok midler til å kjøpe nødvendige varer (mat, husleie, osv), så vil kontantstøtte være en bedre verktøy.
2.) Forklar hvordan under en pandemi eller lignende krise, at ekspansiv pengepolitikk kan føre til lavere priser.
Se seksjon: Pengepolitikk i korona