The Production Function and Productivity

The Machine that Builds the Machine

Source: Tesla Quarterly Report, Q1'20

Ford was the world's first large-scale car company that started the modern car industry.

But the reason that Ford succeeded was not necessarily the quality of the car that Ford produced. Ford's production car, the Model T, was in many cases simpler than many of its competitors. What made the Model T special was the way it was made. Before the Model T, cars were essentially made by hand, with specialized craftmen assembling each car individually.

Ford's big innovation was to produce the Model T on a moving assembly line with standardized parts. Production was divided up into many small parts, which a worker could do quickly and precisely.

The result was that Ford could produce cars quicker and cheaper than their competitors. Because of the standardized parts used, the cars tended also to be more robust and easier to repair.

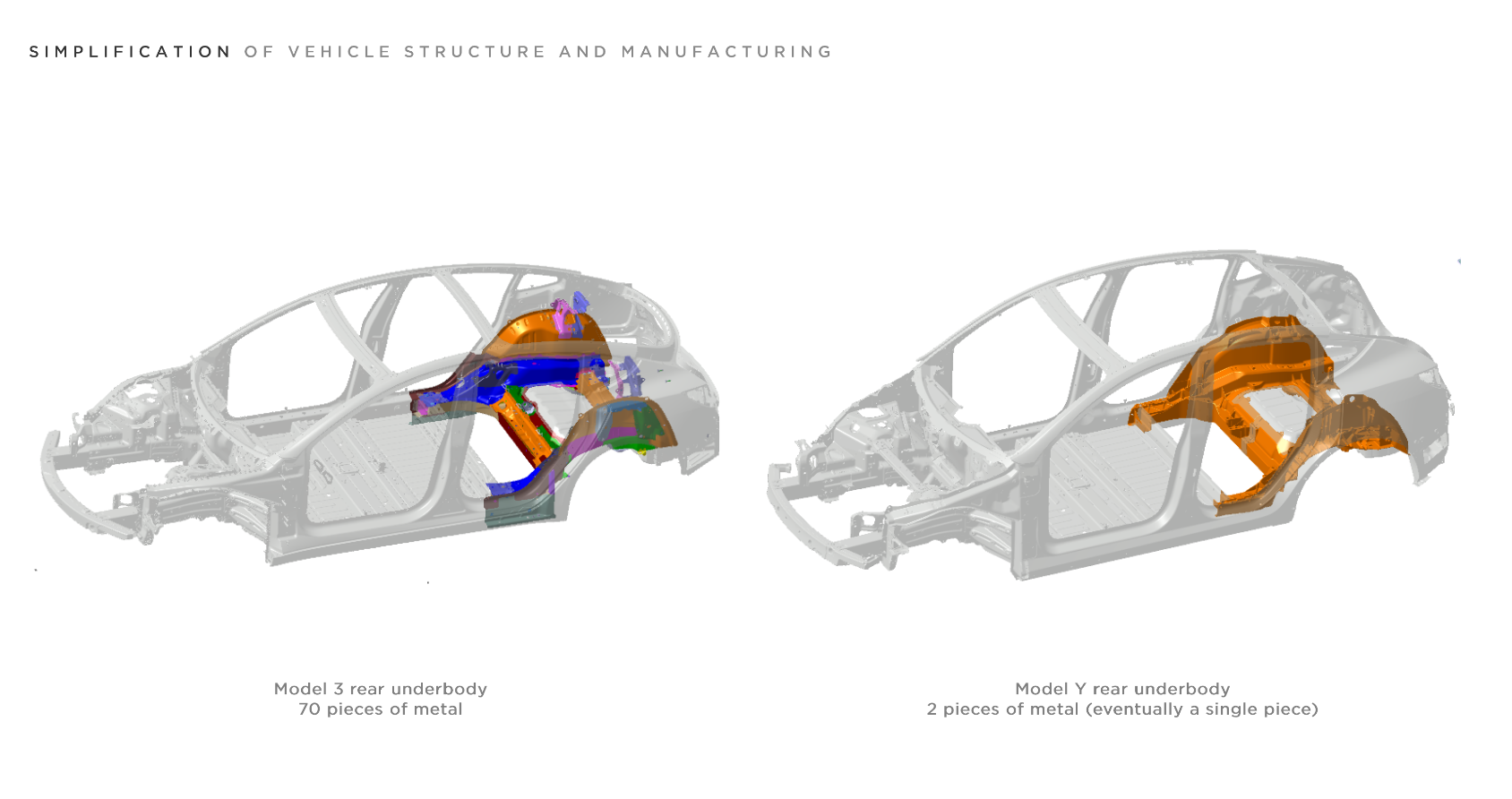
The importance of the production process is also being felt in the move to electric cars. One of the main advantages to an electric car is that they have many fewer costs and will, when factories are optimized, be cheaper to manufacture (though the prices can still be higher than a traditional car because of the cost of the large battery).

Elon Musk has said that the the most important technology that Tesla--the electric car company he runs and helped found--is not the cars themselves, but rather the production process for building them - "the machine that builds teh machine".

Earlier in their production history, Tesla experienced some major problems ramping up the production of their first mass-market Model 3. Musk admitted that they were perhaps too aggressive in introducing automatisation intor their production process. It turns out, there was still the need for a substantial amount of human labor in the process.

Eventually, Tesla was able to work out the problems in their production process and is now able to produce multiple models at a profit. The question that remains is whether Tesla will be able to maintain an advantage in the technology of their cars, but perhaps especially the advantage in their manufacturing, or if their many competitors--both traditional car companies, like ford, as well as new electric start-ups--will catch up.

The production process is complex, but in this lesson we will introduce a simple model of production that allows microeconomists understand some basic trade-offs in the supply-side of our economy.

In this model, we can analyse the interaction between human labor and machine automation, as well as looking at the effect of technological change.

The Production Function

The production function is a model of how we think about the relationship between a firms inputs and their production.

If you have taken a course in management accounting, you may have worked with detailed calculations involving production inputs and outputs. We will have a much simpler set-up. We are not concerned about the particulars about the inputs and costs of any given firm. But instead we want to say something in general about the trade-offs in a production process.

We therefor usually limit ourselves to just broad input categories: Human labor and capital-which includes everything from the factory, production machines, etc.

Cobb-Douglas Production Function

Hire more people Build a new factory

To represent our production function, we often use a mathematical form called the Cobb-Douglas Production Function. This may sound familiar, since we used a version of same type of formula when modelling our utility function in earlier lessons. We can write our production function as:

$$Y=A*K^a*L^{1-a}$$

Here, Y is production, K is capital, and L is labor. A we can think of as a representation of our overall productivity (more on this later). The little a is an indicator on how capital- or labor-intensive our production is. You can think about it as a weight on how labor-intensive a certain production process is.

For example, we can write with parameters:

$$Y=10*K^{0,5}*L^{0,5}$$

Diminishing returns to scale

An important property of the Cobb-Douglas production function that we find to have a good economic intuition is that it displays diminishing returns to scale.

Press the Hire more people button several times. You can see that the point moves up along the curve, but the increase becomes less and less each time. This is what we mean by diminishing returns to scale - the extra production from adding an employee becomes less and less.

The same is true for capital. If we add capital alone (factory, machines, delivery vans, etc) without increasing labor to use them, we get less and less return each time we invest.

Constant returns to scale

With a Cobb-Douglas production function, if you increase capital and labor proportionally, then you also will get a proportional increase in production. So if you double your capital and labor, you will get a doubling of production. This is called constant returns to scale.

Press Hire more people and then Build a new factory. Notice that the increase in production is constant if you continue with this a few times.

Productivity

Source: Tesla Quarterly Report, Q1'20

Increase TFP

Produktivitet

When a company increases their production without increasing the amount of labor they use, we say they have become more productive.

Increased productivity can come from more capital, better technology, improved management or better production techniques.

Productivity in a Cobb-Douglas production function

We can measure productivity by dividing production by the amount of labor L. In our Cobb-Douglas function where we set \(a=1/2\), så kan vi skrive:

$$\frac{Y}{L} = \frac{A*K^{1/2}*L^{1/2}}{L} = A(\frac{K}{L})^{1/2}$$

We can this our production function in capital intensive form since we can interpret (K/L) as capital intensity.

From this equation, we can see that we can increase productivity, \(\frac{Y}{L}\), in two ways:

• Increase the capital intensity (capital per worker \(\frac{K}{L}\)--you can give each employee a new laptop. This is subject to diminishing returns to scale.
• Or increase A: which we call Total Factor Productivity (TFP)

Total Factor Productivity (TFP)

The best way of thinking about TFP is as representing everything that effects productivity except capital.

TFP is most often interpreted as a state of technology, but it can also include factors such as the effectiveness of management.

In our Cobb-Douglas model, we can see that TFP has a proportional effect on production and productivity. If we increase TFP by 50% this leads to a 50% increase in production.

Press the Increase TFP button a few times. The increase in production is constant.

Quiz

Answer True or False about the following statements