Fleksibel valutakurs, konkurranseevne og pengepolitkk
IS-MP i en åpen økonomi med flytende valutakurs
Så langt har vi enten sett på en lukket økonomi der vi ser bort fra import og eksport, eller sett på import og eksport med en implisit antakelse om at vi har en fast valutakurs.
Men virkeligheten er at de fleste utviklet land har en flytende valutakurs der valutakursen blir påvirket av rentenivå, og at internasjonal handel blir påvirket av valutakursen.
Denne modellen blir særlig viktig for land som Norge som har veldig mye internasjonal handel i forhold til BNP.
Vi begynner med litt tilbakeblikk fra forelesning 7.
Vi skal skrive valutakurs som innenlands/utenlandsk. Så valutakursen kronen mot dollaren skriver vi som E= 8kr/dollar.
- Det betyr at når E går opp, så betyr det at kronen svekker seg (depresiering)
- Og når E går ned, så betyr det at kronen styrker seg (appresiering)
Vi husker at vi kan også skrive realvalutakursen som:
$$\epsilon = \frac{EP^*}{P}$$Her ser vi at realvalutakursen forteller oss noe om de relative prisnivåene i et land - hvis du overfører penger til dollar og kjøper en korg med varer i USA, hvor mye får du relativt til den samme korgen av varer i Norge.
Udekket renteparitet med nominelle størrelser kan vi skrive som:
$$i \approx i^* + g^e_E$$Der \(g^e_E = \frac{E^e-E}{E}\)
Tilsvarende formula med realrente og realvalutakurs er:
$$r \approx r^* + g^e_{\epsilon}$$Som vi også kan skrive som:
$$r \approx r^* + \frac{\epsilon^e-\epsilon}{\epsilon}$$Vi kan skrive dette om så at realvalutakursen er på venstre siden:
$$r-r^* = \frac{\epsilon^e}{\epsilon} - 1$$ $$\epsilon = \frac{\epsilon^e}{r-r^*+1}$$IS-sammenhenget i en åpen økonomi og netto-eksportfunksjonen
Netto-eksport funksjonen
For å inkludere en internasjonal sektor i vår modell, så skal vi først skape en netto-eksportfunksjon:
$$NX = q^*Y^* - \frac{n}{\epsilon}-qY$$Dette sier at størrelsen på nettoeksport er basert på en kombinasjon av utenlandsk BNP på eksport, innenlandsk bnp på import og realvalutakursen (relative prisene).
Vi bruker vår definisjon for udekket renteparitet og bytter ut realvalutakursen, \(\epsilon\)
$$NX = q^*Y^*-\frac{n}{\epsilon^e}(r-r^*+1)-qY$$IS-sammenhenget
Nå kan vi skrive IS-sammenhenget for en åpen økonomi.
Vi begynner med å skrive ut aggregert etterspørsel:
$$Z=C+I+G+NX$$Vi har som vanlig vår konsumfunksjon, investeringsfunksjon, og nå også vår nettoeksportfunksjon:
$$C=cY+b$$ $$I = I_0 -vr$$ $$NX = q^*Y^*-\frac{n}{\epsilon^e}(r-r^*+1)-qY$$Som før, så definerer vi \(c=(1-t)a\)
Og vi setter \(T_0=0\) fra nettoskattfunksjonen og \(b=0\) fra konsumfunksjonen for å forenkle.
Øvelse
Utlede IS-sammenhenget i en åpen økonomi
Vi skriver aggregert etterspørsel som:
$$Z= C+I+G+NX$$ $$Z = cY + I_0 - vr + G + q^*Y^*-\frac{n}{\epsilon^e}(r-r^*+1)-qY$$Vi setter Y=Z og samler Yene
$$Y = cY + I_0 - vr + G + q^*Y^*-\frac{n}{\epsilon^e}(r-r^*+1)-qY$$ $$Y-cY +qY = I_0 - vr + G + q^*Y^*-\frac{n}{\epsilon^e}(r-r^*+1)$$ $$Y(1-c+q) = I_0 - vr + G + q^*Y^*-\frac{n}{\epsilon^e}(r-r^*+1)$$ $$Y = \frac{1}{1-c+q}[I_0 + G + q^*Y^*+\frac{n}{\epsilon^e}(r^*-1)] - \frac{1}{1-c+q} (v + \frac{n}{\epsilon^e})r$$Her er det litt å ta inn, men en viktig ting å ta ut av denne ligningen er at vi har to mekanismer for hvordan renten kan påvirke aggregert produksjon i likevekt.
- Gjennom nettoexport og URP.
- Gjennom investering.
I figuren under viser likevekten i en åpen økonomi. Likevektsbetingelsen er representert med den røde 45-graders linjen.
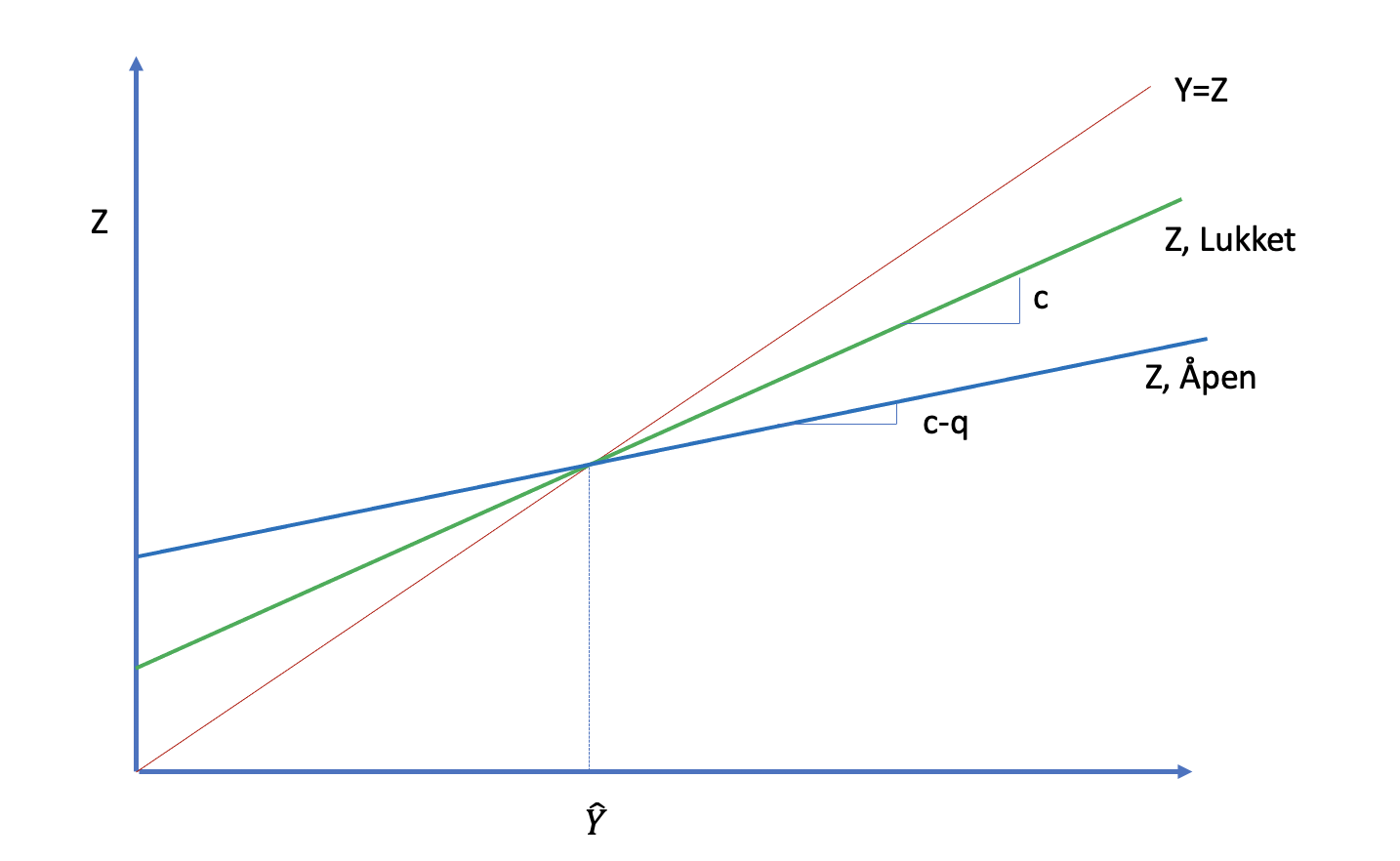
Aggregert etterspørsel i en lukket økonomi er representert med den grønne linjen der stigningsgraden er liten c – den marginale konsumtilbøyeligheten
Mens aggregert etterspørsel i en åpen økonomi er den blåe linjen, der stigningsgraden er c-q, der q er den marginale importtilbøyelighet. Legg merke til at helningen av aggregert etterspørselskurven er mindre bratt. Dette forteller oss at det er et svakere forhold mellom aggregert etterspørsel og inntekt. Intuisjonen er at høyere inntekt vil føre til mer etterspørsel etter import, som kan tolkes som en "lekasje" av etterspørsel til utlandet.
En viktig implikasjon av en mindre bratt aggregert etterspørselskurv er en lavere multiplikatør i vår IS-forhold. Under en sjokk til aggregert etterspørsel, for eksempel, hvis offentlig konsum plutselig ble mindre, så ville effekten på produksjon i likevekt i en åpen økonomi være mindre enn i en lukket økonomi, som er illustrert i figuren under.
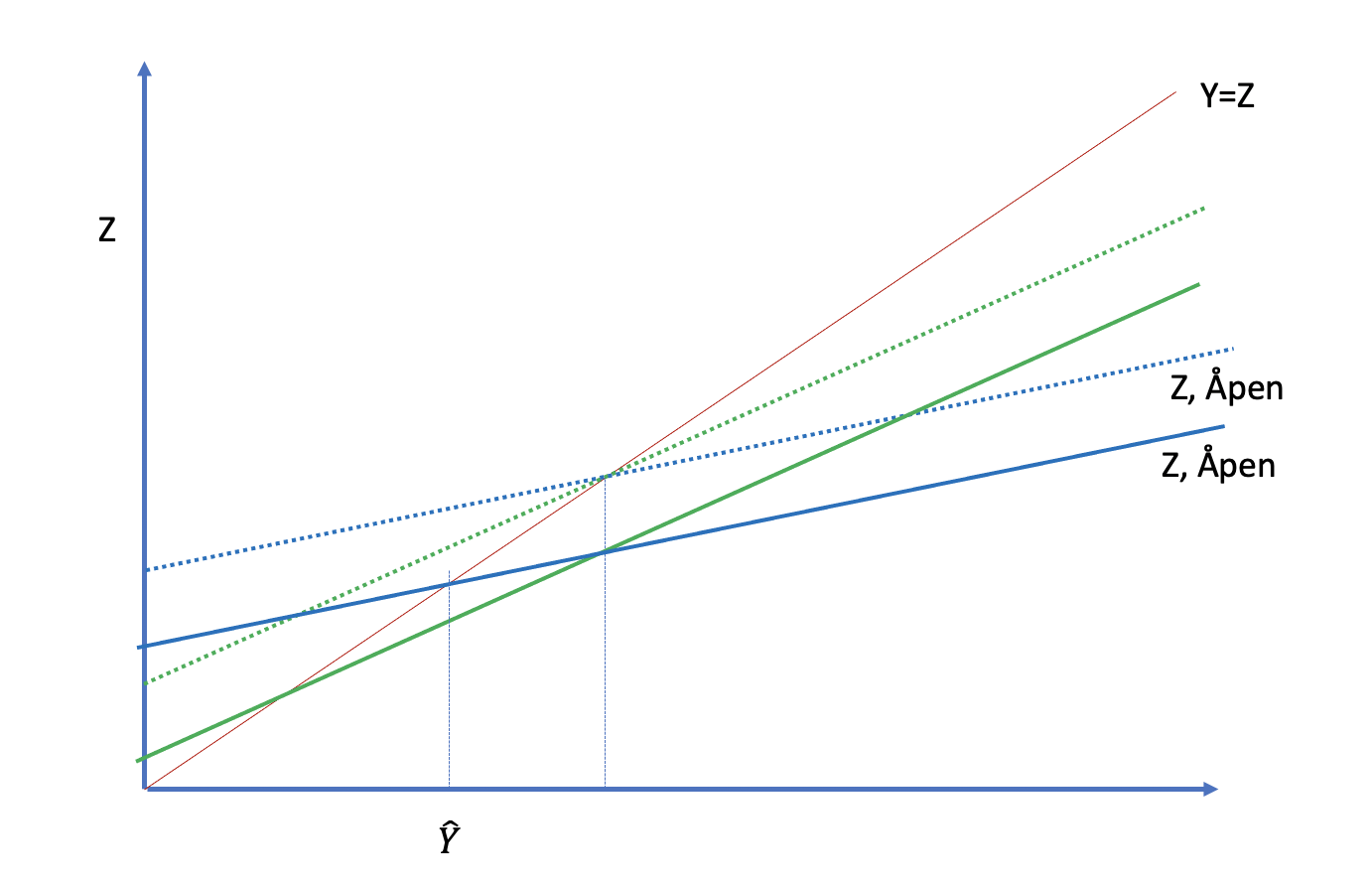
Vi kan vise hvorfor ved å se på multiplikatøren i vår åpen økonomi likevekt:
$$M=\frac{1}{1-c+q}$$En tall eksempel, hvis c, konsumtilbøyeligheten, er likt .5 og q, importtilbøyeligheten, er likt .1
Så er multiplikatoren 2 i en lukket økonomi og ca. 1.67 i en åpen økonomi.
Grunnen for at multiplikatoren er mindre i en åpen økonomi er det vi kaller for importlekkasje.
La oss se på en scenario der offentlig utgifter øker- det vil si en ekspansiv finanspolitikk.
Når etterspørsel fra offentlig utgifter øker, så øker produksjon.
Med høyere produksjon og inntekt, så øker privat konsum, og det fører videre til høyere produksjon
Men med høyere produksjon kommer også høyere import og derfor mindre netto-eksport.
Dette har en negativ effekt på produksjon som demper effekten av økt konsum.
Oppsummering: Likevekt i en åpen økonomi med flytende valutakurs
Tall eksempel
Vi tar utgangspunkt i en normal konjunktursituasjon der BNP er likt normalt BNP i en åpen økonomi med flytende valutakurs.
Vi har samme realrente i hjemlandet som i utlandet:
$$r= r^*=0,02$$Realvalutakursen er lik forventet realvalutakursen i fremtiden:
$$\epsilon = \epsilon^e = 1$$Og vi kan beskrive økønomien med følgende konsum-, investerings- og nettoeksportfunksjoner:
$$C=a(1-t)Y+b$$ $$I=I_0 - vr$$ $$NX=q^*Y^*-\frac{n}{\epsilon^e}(r-r^*+1)-qY$$Og vi har følgende størrelser og parametere:
- t=0,25
- G=25
- \(I_O = 22\)
- v=100
- \(a=\frac{2}{3}\)
- b=5
- n=100
- \(q^*Y^* = 150\)
- q=0,5
a.) Hva er multiplikatøren? Ville den vært større eller mindre sammenlignet en lukket økonomi?
b.) Hva er Y i likevekt? Hva er C og I og NX?
c.) Sentralbanken øker renten til \(r=0,03\). Hva er Y, C, I, \(\epsilon\) og NX i likevekt?
Eksempel oppgave I: Endring i forventet valutakurs
Brexit har ført til en endring i forventet valutakurs mellom Norkge og EU (NOK/EUR). Markedet forventer at euroen skal svekke seg i forhold til den norske kronen. Vil dette ha en effekt på dagens valutakurs? Vil det påvirke likvekten i vår konjunkturmodell? Eventuelt vis med en IS-MP figur.
Eksempel oppgave II: rentegulv
Gå ut i fra at i utgangspunktet så ligger den realrenten på 0 mens inflasjon er 1%. Økonomien er i en lavkonjunkter.
Kan landets sentralbank senke realrenten under 0? Eventuelt hva er rentegulvet?
Landet er fortsatt i lavkonjunktur etter å ha nådd rentegulvet (likviditetsfelle). Sentralbanken beslutter derfor å sette en nedre grense for valutakursen og kjøper utenlandsk valuta for å svekke kronen. Hvordan påvirker dette likevekt. Vis i en IS-MP figur.
Øvelse
Etter at sentralbanken publiserer sin pengepolitisk rapport, øker det forventningene for framtidige rentenivå. Kan dette påvirke økonomien på kort sikt? Vis i en IS-MP diagram. Forklar.
Når forventet rente, \(r^e_{t+1}\), øker så fører det til at forventet realvalutakursen styrker seg (via udekket renteparitet). Og det vil føre til at dagens realvalutakurs vil også styrke seg.
En sterkere valuta vil føre til mindre eksport og høyere import. Det vi da føre til høyere aggregert etterspørsel og høyere pro
Fast eller flytende valutakurs
MM K10.3
Fram til 2001, hadde Norge en fast valutakurs der målet var å holde verdien av kronen konstant sammenlignet med en vektet gjennomsnitt av valutaene til norges handelspartnere.
Sentralbankens hovedrolle med en fast valutakurs er å opprettholde valutakursen.
Derfor mister man evnen til å drive selvstendig pengepolitikk.
Hvis Norge Bank, for eksempel skulle senke renten mer enn det i tyskland, som i praksis var ankerlandet, så ville udekket renteparitet si at valutakursen burde også endre seg.
Fast valutakurs har noen fordeler: det kan være gunstig å ha en stabil valutakurs hvis man driver internasjonal handel.
Men det kan også være store ulemper hvis økonomiske sjokk slår ut på ulike måte i hjemmelandet og ankerlandet.
Dette kalles asymmetrisk sjokk.
Assymetriske sjokk.
Figuren viser problemet med en fast valutakurs når det finnes asymmetriske sjokk.
Her har vi to land, hjemmelandet (la oss si Norge), og landet som vi fester valutakursen til, la oss si tyskland.
Hjemmlandet må følge ankerlandets pengepolitikk, og derfor har de en felles MP linje som setter realrenten, r.
La oss si at i utgangspunktet ligger begge landene på sin potensielt BNP og renten, r, er neutral for begge landene.
En asymmetrisk sjokk, er en sjokk som slår ut på ulike måter i de to landene.
En eksempel kunne vært at oljeprisen faller merkant.
Dette ville føre til en negativ sjokk i Norge, et land som produserer olje, men et positivt sjokk i Tyskland som importerer og forbruker olje.
For å oppretteholde potensielt BNP i tyskland, så burde man sette opp renten så at økonomien ikke overoppheter.
Men i Norge ville vi egentlig ønske å gjøre det motsatte.
I denne situasjonen ville en fast valutakurs føre til en pengepolitikk som egentlig forverrer konjunkturen.
Oppsummering oppgave: Fast valutakurs
Norge bestemmer å innføre fast falutakurs med Eurosonen.
a.) Hvorfor fører dette til at Norge mister sin evne å drive selvstendig pengepolitikk?
b.) Oljeprisen går plutselig ned med 30$ fatet. Dette har en positiv effekt på Eurosonen (som importerer olje) men en negativ effekt på Norge (som eksporterer olje). Vis effekten med en IS-MP figur for både Norge og eurosonen.
c.) Hva blir antakeligvis den pengepolitiske responsen til den Europeiske sentralbanken?
Devalueringsforventninger og spekulasjonsangrep
De fleste land som har hatt fast valutakurs har opplevd å måtte svekke sin egen valuta, eller å tillate at den svekkes på valutamarkedet.
Når en sentralbank tillater en fast valutakurs til å svekkes, kalles det en devaluering.
Hvis valutakursen er fleksibel og svekkes på markedet så heter det en depresiering.
Den praktiske effekten er det samme.
Noen ganger er det sånt at en sentralbank blir tvunget til å devaluere sin valuta på grunn av et spekulasjonsangrep.
Et spekulasjonsangrep handler om forventninger og sentralbankens troverdighet.
Troverdi og ikke troverdi fast valutakurs
En spekulasjonsangrep er når markedsaktører forventer en devaluering og derfor låner de valuta (for eksempel kroner) for da å selge kronene på valutamarkedet ("shortsalg"). Hvis valutaen blir devaluert, så kan de kjøpe tilbake valutaen billigere senere, betale tilbake sitt lån og komme ut med en fortjenst.
En troverdig fast valutakurs er en valutakurs som er bygget på en lang historie uten devaluering.
Sentralbanken har vist gjennom historien at de har forpliktet seg 100 prosent til å etablere en fast valutakurs, og det er ingen i markedet som tror at sentralbanken kommer til å devaluere valutaen. Det er derfor ingen som prøver å shortselge valutaen i en spekulasjonsangrep.
Da kan man skrive situasjonen som:
$$E=E^e$$og udekket rentepartitet blir:
$$(1+i) \times \frac{E^e}{E} => i=i^*$$Det vil si at forventet valutakurs er det samme som den etablerte, faste valutakurset, E. Udekket renteparitet blir kollapser derfor til å si at innenlandske og utenlandske renter blir det samme.
Men hvis sentralbanken oppleves som svak og den faste valutakursen er ikke sett som troverdig, så kan det fort etableres en forventning om at sentralbanken kommer til å devaluere valutaen. Dette blir da en ikke troverdig fast valutakurs.
Når markedet forventer en devaluering, så tiltrekker det shortsalg av valutaen.
Sentralbanken må da inn i markedet og kjøpe sin egen valuta med sine reserver av utenlandsk valuta for å prøve å oppretteholde valutaen.
Hvis de går tom for utenlandsk valuta, så har de bare to valg:
De må enten sette opp renten for å prøve å opprettholde udekket renteparitet. Eller, så kan de devaluere.
På denne måten kan bare forventningen av en devaluering føre til en faktisk devaluering.
Det gir også spekulanter et insentiv til å danne forventninger i markedet.
Denne situasjonen kan vi skrive som:
$$E^e>E$$Og dermded blir udekket renteparitet:
$$(1+i) = (1+i^*) \frac{E^e}{E} => i> i^*$$Pengunion
Hvis man ønsker en fast valutakurs, men har problemer med å etablere troverdighet, en mulig løsning kan være pengeunion.
Den mest kjent pengeunionen er eurosonen, der alle landene deler en felles valuta: euroen.
Det finnes noen betydelige fordeler med pengeunion.
Når man slipper å veksle penger så betyr det færre kostnader med internasjonal handel: noe som vi kan kalle transaksjonskostnader.
Med en felles valuta er det også lettere å sammenligne priser i ulike land, dette kan føre til mer konkurranse mellom land og en mer effektiv marked.
Men som med fast valutakurs, finnes det også noen store ulemper.
Den største er at man ikke kan bruke pengepolitikk til å takle asymmetriske sjokk.
Om et land burde være i en pengeunion eller ikke handler da om landet opplever mange asymmetriske sjokk og hvor fleksibel det landet er i å bruke andre verktøy, som finanspolitikk, til å motarbeide asymmetriske sjokk.
Inflasjonsmål for pengepolitikk
MM K11.2
Fram til 1990-tallet hadde flere land, inkludert norge, fast valutakurs.
Sentralbankens hovedrolle var dermed å selge og kjøpe valuta for å opprettholde denne faste valutakursen.
Men kombinasjonen av en deregulert finanssystem, fri flyt av kapital mellom land og fast valutakurs førte til makroøkonomisk ustabilitet og høy inflasjon, der sentralbanken hadde lite makt.
I løpet av 1990-tallet, byttet norge over til en regime med flytende valutakurs og inflasjonsmål for pengepolitikk, der sentralbanken fikk en mye viktigere rolle
Dette har ført til større makroøkonomisk stabilitet og lavere inflasjon.
Inflasjonsmål for pengepolitikk er karakterisert ved at de politiske myndighetene delegerer store deler av jobben av å styre økonomien på kort sikt til sentralbanken.
De politiske myndighetene bestemmer et mål for inflasjon: som nå ligger på 2 prosent i norge, men sentralbanken har operasjonell uavhengighet.
Det betyr at de kan bestemme selv hvordan de tar i bruk sine virkemidler til å kontrollere inflasjon, som å justere styringsrenten og gjøre åpen-markedsoperasjoner for å styre pengetilbud.
Siden kronen er tillatt å flyte og bestemmes fritt av markedet, behøver ikke banken å gripe inn i valutamarkedet. De kan derfor fokusere på sitt oppdrag av å holde inflasjonsraten stabil
I Norge, og flere andre land, så har sentralbanken også mål av å begrense fluktuasjonene i produksjon og sysselsetting.Det vil si at de må noen ganger avveie målene om stabil inflasjon og et null produksjonsgap.
Åpenhet og forutsigbarhet
Staten delegerer noe politisk makt til Norges Bank men i retur, forplikter Norges Bank seg til åpenhet og forutsigbarhet.
Dette har også store makroøkonomiske fordeler
En viktig forventning til Norges Bank er at de forklarer grundig grunnlaget sitt for rentesetting.
Dette gjør de kvartalsvis gjennom dokumentet pengepolitisk rapport (som er åpent tilgjengelig på nettsiden til Norges Bank).
Norges Bank skal også kommunisere sine intensjoner og løpende vurderinger.
For eksempel, om de forventer at de skal sette opp renten i framtiden, så skal dette kommuniseres på en tydelig måte.
Åpenhet og forutsigbarhet er en viktig del av vellykket pengepolitikk.
Som vi har sett, så er riktige forventninger en veldig viktig del av makroøkonomisk stabilitet.
Hvis sentralbanken er vellykket i å få aktører som bestemmer både priser og lønn til å forvente at inflasjonen blir nær inflasjonsmålet, så blir det også i praksis lettere å oppnå inflasjonsmålet!
Åpenhet om prosesser vil også ha en effekt på finanspolitikk.
Hvis politikerene vet at ekspansiv finanspolitikk kan føre til høyere renter fra Norges Bank som i sin tur vil ha en effekt på valutakurs og konkurranseevne til norsk økonomi, så vil det kanskje føre til en mer ansvarlig finanspolitikk.
Fleksibel inflasjonsstyring
Vi kan generelt definere tre strategier for en sentralbank som skal drive med inflasjonsstyring.
Den første er streng inflasjonsstyring.
Her har sentralbanken bare et mål: å oppnå stabil inflasjon, det vil si å oppnå inflasjonsmålet. Sentralbanken skal, eksplisitt, ikke bry seg om effekten på produksjonsgapet eller arbeidsledighet.
Det motsatt av dette er streng produksjonsstyring. Her skal målet være utelukkende å prøve å styre produksjonsgapet mot null. Man skal ikke prøve å kontrollere inflasjon utover å stabilisere produksjonsgapet.
En mellom-strategi, som Norges Bank og de fleste andre sentralbanker utfører, heter fleksibel inflasjonsstyring.
Her skal man avveie mellom inflasjonsmål og produksjonsgap.
Hvis det er et etterspørselssjokk i økonomien, så har ikke det så mye å si, siden begge av disse målene vil dra i samme retning.
En negativ etterspørselssjokk (la oss si et fall i oljeprisen som fører til mindre investering) vil føre til negativ produksjonsgap og inflasjon som er lavere enn målet.
Men hvis det skjer et kostnadssjokk, som fører til høyere eller lavere priser uten nødvendigvis å påvirke produksjon eller kanskje til og med påvirke produksjon i motsatt retning, så blir det vanskeligere.
Høyere rente vil, for eksempel, bekjempe høyere inflasjon, men kan øke produksjonsgapet.
Her blir jobben til sentralbanken vanskeligere, og de må avveie kostnadene av inflasjon mot kostnadene av produksjonsgapet.
Quiz
Svar Sant eller Usant om følgende påstander
1.) I k.7, skrev vi udekket renteparitet (URP) som \(i=i^* + g^e_E\). a.) Forklar hva URP sier og forklar, intuitivt, logikken bak denne formellen. b.) I k.10 skriver vi URP som \(r=r^* + g^e_{\epsilon}\), der r er realrenten og \(\epsilon\) er realvalutakursen. Hvilken forutsetning bruker vi til å forsvare bruken av denne formen av URP?
2.) Når vi introduserer en fleksibel valutakurs i vår konjunkturmodell, så kan renten påvirke aggregert etterspørsel via to kanaler. Forklar hva de kanalene er.
3.) Vi kan skrive en nettoeksport funksjon som følgende:
\(NX = q^*Y^* - \frac{n}{\epsilon^e}(r-r^*+1) -qY\).
Forklar hvordan denne formelen representerer nettoeksport under en flytende valutakurs. Inkluder en tolkning av parameterene \(q^*\), \(q\) og \(n\).
4.) Vi beskriver en økonomi som følgende:
\(Z=C + I + G + NX\), der NX er nettoeksport
\(C=0,5(Y-T)\)
\(T=0,1Y\)
\(I = 25 - 100*r\)
\(NX = 150 - \frac{100}{\epsilon^e}(r-r^*+1)-0,2Y\)
Videre, sier vi at \(\epsilon^e=1\) og at realrenten i hjemlandet er likt realrenten i utlandet, \(r=r^*=0,05\) og at G=25.
a.) Hva er Y, C, I og NX i likevekt?
På grunn av koronaviruset, frykter markedet at valutakursen kommer til å svekke seg, så at forventet valutakursen øker til \(\epsilon^e=1,1\).
b. Forklar mekanismen som gjør det mulig for at en endring i forventet valutakurs har en realøkonomisk effekt.
c. I vår modell, vil endret forventet valutakurs påvirke nettoeksport via to kanaler. Forklar hva de er.
d. Finn Y, C, I og NX i likevekt.
5.) Gå ut i fra en modell av en åpen økonomi med flytende rente (Norge, for eksempel). Vi tar utgangspunkt i en modell i likevekt og der BNP er på sin normalt nivå. La oss si at nytt informasjon kommer som fører til at markedet nå forventer at renten i utlandet (Europa/USA) kommer til å øke. Ut i fra vår åpen økonomi IS-MP modell, kan dette ha en realøkonomisk effekt på Norges økonomi? Forklar mekanismen. Vis effekten i en IS-MP figur.
2.) Når vi introduserer en fleksibel valutakurs i vår konjunkturmodell, så kan renten påvirke aggregert etterspørsel via to kanaler. Forklar hva de kanalene er.
Renten kan påvirke aggregert etterspørsel gjennom den vanlige investeringskanalen - lavere rente fører til økt investering
Nå kan renten også føre til økt aggregert etterspørsel via økt netto-eksport. Lavere rente vil føre til en svakere krone (udekket renteparitet), og det vil føre til lavere import og økt eksport.
3.) Vi kan skrive en nettoeksport funksjon som følgende:
\(NX = q^*Y^* - \frac{n}{\epsilon^e}(r-r^*+1) -qY\).
Forklar hvordan denne formelen representerer nettoeksport under en flytende valutakurs. Inkluder en tolkning av parametrene \(q^*\), \(q\) og \(n\).
Det er tre ledd i formelen, og vi kan ta de en-for-en:
- \(q^*Y^*\) representerer effekten av utenlandsk etterspørsel, der \(q^*\) er den marginale eksport-tilbøyeligheten - det vil si, at når utenlandsk inntekt øker (\(Y^*\)) så indikerer \(q^*\) hvor mye eksport øker.
- \(qY\) representerer effekten av etterspørsel etter import på grunn av økt inntekt/BNP (Y). Her er \(q\) marginale import-tilbøyelighet - det vil is at det indikerer hvor mye import øker når BNP øker.
- \(\frac{n}{\epsilon^e}(r-r^+1)\) er effekten fra valutakursen, som kommer fra udekket renteparitet.
- \(\epsilon^e\) er forventet framtidig valutakurs. Hvis den øker (valutakursen svekker seg), så vil leddet bli mindre (negativ), og føre til en høyere netto-eksport.
- n er en parameter som indikerer hvor sterkt valutakursen påvirker netto-eksport.
- \((r-r^*)\) indikerer renteavik mellom hjemlandet og utlandet. Hvis renten er høyere i utlandet, så vil det føre til en svakere (høyere) valutakurs og økt netto-eksport.
4.) Vi beskriver en økonomi som følgende:
\(Z=C + I + G + NX\), der NX er nettoeksport
\(C=0,5(Y-T)\)
\(T=0,1Y\)
\(I = 25 - 100*r\)
\(NX = 150 - \frac{100}{\epsilon^e}(r-r^*+1)-0,2Y\)
Videre, sier vi at \(\epsilon^e=1\) og at realrenten i hjemlandet er likt realrenten i utlandet, \(r=r^*=0,05\) og at G=25.
a.) Hva er Y, C, I og NX i likevekt?
Vi setter opp vår likevekt:
\(Y=Z\)
\(Y=C+I+G+NX\)
\(Y=0,5(Y-T) + 25 - 100*r + G + 150 - \frac{100}{\epsilon^e}(r-r^*+1)-0,2Y\)
Setter in nettoskattfunksjonen
\(Y=0,5(Y-0,1Y) + 25 - 100*r + G + 150 - \frac{100}{\epsilon^e}(r-r^*+1)-0,2Y\)
Samler alle Y-leddene på den ene siden
\(Y-0,5Y+0,05Y+0,2Y = 25 +G + 150 - 100*r - \frac{100}{\epsilon^e}(r-r^*+1)\)
Trekker ut Y og samler r-leddene
\(Y(1-0,5+0,05+0,2) = 25 +G + 150 - r(100 + \frac{100}{\epsilon^e}) - \frac{100}{\epsilon^e}(1-r^*)\)
\(Y(0,75) = 25 +G + 150 - r(100 + \frac{100}{\epsilon^e}) - \frac{100}{\epsilon^e}(1-r^*)\)
\(Y=\frac{4}{3}[175 + G - r(100 + \frac{100}{\epsilon^e}) - \frac{100}{\epsilon^e}(1-r^*)]\)
Setter inn parametrene og eksogene variablene:
\(Y=\frac{4}{3}[175 + 25 - 0,05*(100 + \frac{100}{1}) - \frac{100}{1}(0,95)]\)
\(Y=\frac{4}{3}[200 - 0,05(200) -95]\)
\(Y=\frac{4}{3}*95=126,7\)
\(T=0,1Y=12,7\)
\(C=0,5(126,7-12,7)=57\)
\(I = 25 - 100*r = 20\)
\(NX = 150 - \frac{100}{\epsilon^e}(r-r^*+1)-0,2Y\)
\(NX = 150 - 100(0,05-0,05+1) - 0,2*126,7 = 24,7\)
Vi kan sjekke vårt svar ved å se om C+I+G+NX=Y
På grunn av koronaviruset, frykter markedet at valutakursen kommer til å svekke seg, så at forventet valutakursen øker til \(\epsilon^e=1,1\).
b. Forklar mekanismen som gjør det mulig for at en endring i forventet valutakurs har en realøkonomisk effekt.
Via udekket renteparitet kan en forventet endring i realvalutakursen påvirke dagens valutakurs. En svakere valutakurs vil føre til økt eksport og derfor økt etterspørsel.
c. I vår modell, vil endret forventet valutakurs påvirke nettoeksport via to kanaler. Forklar hva de er.
Den første er som i b - via lavere realvalutakurs som øker eksport.
Den andre er indirekt og i motsatt retning via import: en lavere realvalutakurs vil føre til økt eksport, som fører til høyere innetekt/BNP, og høyere BNP fører til høyere import.
Den første kanalen vil være større.
d. Finn Y, C, I og NX i likevekt.
Vi begynner med vår likevektsligning:
\(Y=\frac{4}{3}[175 + G - r(100 + \frac{100}{\epsilon^e}) - \frac{100}{\epsilon^e}(1-r^*)]\)
Som nå blir:
\(Y=\frac{4}{3}[175 + G - r(100 + 90,9) - 90,9(1-r^*)]\)
\(Y=\frac{4}{3}[200 - 0,05(190,9) - 90,9(0,95)]\)
\(Y=\frac{4}{3}[104,1]\)
\(Y=\frac{4}{3}[104,1]=138,8\)
\(T=0,1*138,8=13,9\)
\(C=0,5(138,8-13,9)=62,5\)
\(I=20 (uendret)\)
\(NX = 150 - \frac{100}{\epsilon^e}(r-r^*+1)-0,2Y\)
\(NX = 150 - 90,9(0,05-0,05+1) - 0,2*138,8 = 31,3\)
Vi kan igjen sjekke vårt svar ved å se om C+I+G+NX=Y
Nå, la merke til at denne eksempelet ikke er særlig realistisk. Den eneste måten koronaviruset påvirker økonomien er via svekket forventet valutakurs (som er positiv for netto-eksport). I virkeligheten har koronakrisen hatt en veldig negativ effekt på norsk økonomi.
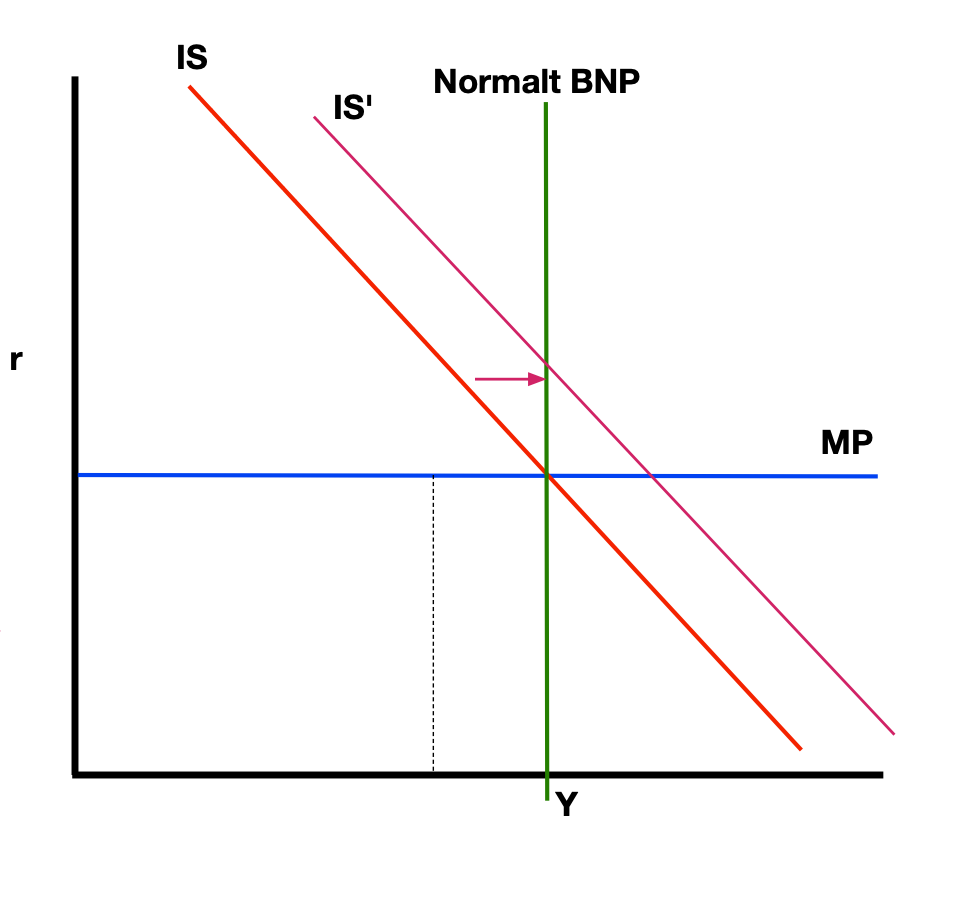
5.) Gå ut i fra en modell av en åpen økonomi med flytende rente (Norge, for eksempel). Vi tar utgangspunkt i en modell i likevekt og der BNP er på sin normalt nivå. La oss si at nytt informasjon kommer som fører til at markedet nå forventer at renten i utlandet (Europa/USA) kommer til å øke. Ut i fra vår åpen økonomi IS-MP modell, kan dette ha en realøkonomisk effekt på Norges økonomi? Forklar mekanismen. Vis effekten i en IS-MP figur.
Ja, det kan ha en realøkonomisk effekt.
Forventning til økt rente i utlandet, fører til forventninger til en svakere innenlandsk valutakurs, som da fører til en svakere valutakurs via udekket renteparitet. Det fører til økt nette-eksport. Vi viser dette som at IS-kurven flyttes mot høyre.