Arbeidsmarkedet

I diskusjonen om IS-MP modellen, så snakket vi om en normalt- eller potensielt-BNP som speilet et BNP-nivå som er bærekraftig på langsikt.

I vår kortsiktig IS-MP modell, så tillater vi BNP til å gå over normalt-BNP, men vi sa også at på lengre sikt vil det føre til inflasjon.

Men hva er mekanismen for hvordan en for høy BNP / for lav rente kan føre til inflasjon? Og hvordan påvirker det måten vi driver pengepolitikk?

Det er spørsmålene vi kommer til å se på i denne forelesningen og som vi kommer til å bygge på i senere deler av kurset.

Vi skal starte ved å se på arbeidsmarkedet, siden det er ofte her man finner kilden til økt press på priser i økonomien.

Strukturelle Arbeidsledighet

MM K6.4

Arbeidsledighet er en av de viktigste makroøkonomiske indikatørene og det er en viktig faktor i seg selv: Folk flest ønsker å jobbe og tjene penger.

Høy arbeidsledighet er en sterk indikatør på at økonomien gjør en dårlig jobb ved å utnytte ressurser. Høy arbeidsledighet er også en indikatør på at et land har potensial som ikke blir benyttet.

Klassifikasjon av arbeidsledighet

Vi kan dele arbeidsledighet i to kategorier

• Syklisk: Der arbeidsledigheten går opp og ned sammen med makroøkonomiske konjukturer. For eksempel, arbeidsledighet i Norge har en tendens å gå opp når oljeprisen går ned.
• Strukturell ledighet: Viktigere på lang sikt er strukturell ledighet. Dette er arbeidsledighet som er vedvarene over flere sykler. Det er en indikasjon på noe mer fundementalt om en økonomi og hvordan den er organisert.

Strukturell arbeidsledighet

Selv de mest effektive og best organiserte markedsøkonomier har noe arbeidsledighet, og denne formen av strukturell arbeidsledighet kan vi kalle for friksjonsledighet

Friksjonsledighet: Det tar tid for de arbeidsledige og arbeidsgivere med ledige jobber å finne hverandre («Matching costs»)

Høye real-lønninger

• Minstelønn
• Effektivitetslønn
• Markedsmakt

Den andre hovedgrunnen for høy strukturell arbeidsledighet er høye real-lønninger. Det vil si, at hvis lønningene var lavere, så kunne man også fått lavere arbeidsledighet. Det finnes flere grunner for at real-lønningene kan holdes kunstig høyt. - Minstelønn lover og reguleringer i land - Effektivitetslønn: ideen at arbeidsgivere betaler mer enn de strengt tatt må for å beholde de beste arbeiderne. - Arbeidsgiverne har markedsmakt og det fører til høyere priser som dermed også fører til høyere lønninger. -->

Friksjonsledighet

Friksjonsledighet er ideen at det er alltid en viss «churn», eller dynamikk i økonomien.

Det vil si, nye selskaper blir etablert og gamle legges ned. Noen selskaper må kutte mens andre prøver å ekspandere.

Selv for noen som har riktig utdanning, god erfaring og personlighet, så kan det ta tid før de finner riktig arbeidssted for dem.

På samme måte, et selskap som tilbyr attraktive betingelser kan bruke litt tid å finne riktig kandidat.

Arbeidsgivere har begrenset informasjon på søkere, så de må bruke mye tid og resurser på å finne riktig kandidat

På en hver tid, har man da en gruppe mennesker som går fra en jobb til den andre og blir derfor telt som arbeidsledige, uten at det nødvendigvis er noe som er dårlig.

Det speiler bare at økonomien er dynamisk og at det kan ta litt tid å gå fra den ene jobben til den andre.

Det kan til og med være positivt: Hvis man bruker ekstra tid på å finne riktig arbeidsplass, så kan man kanskje være mer produktiv i den arbeidsplassen.

Ledighetstrygd kan også påvirke friksjonsledighet. For eksempel gjøre det lettere for søkere til å bruke mer på å lete etter jobb, og dermed føre til bedre matching av søkere og arbeidsgivere.

Friksjonsledighet: oppsummering

• Det tar tid og arbeid å matche riktig jobb med riktig arbeidstaker
• Arbeidsgiver har begrenset informasjon
• Kontinuerlig endringer og omstillinger (Teknologi, konjuktur, globalisering, osv)
• Effekten av ledighetstrygd.

Effektivetslønn er ideen at arbeidsgivere gir høyere enn markedslønn for å beholde de beste arbeiderne og gi insentiv til arbeiderne til å jobbe hardere.

En kjent eksempel er Henry Ford når han begynte å produsere Model T bilene på 1910-tallet. Ford økte lønningene til 5 dollar dagen, noe som var mye høyere enn vanlig lønn på det tidspunktet.

Ideen er at hvis det er vanskelig å oppdage innsats på jobben så har arbeidstakere en insentiv til å skulke og ikke jobbe hardt. Hvis de får markedslønn og blir tatt, så er det ikke farlig siden de kan finne en lignende jobb med lignende lønn en annen plass.

Men hvis man tilbyr høyere lønn, så er kostnaden av å miste jobben mye høyere, så man har et insentiv til å jobbe hardt så at man beholder jobben.

Med andre ord, med høy lønn så har man også mer å tape.

Effektivitetslønn

Effektivetslønn er ideen at arbeidsgivere gir høyere enn markedslønn for å beholde de beste arbeiderne og gi insentiv til arbeiderne til å jobbe hardere.

En kjent eksempel er Henry Ford når han begynte å produsere Model T bilene på 1910-tallet. Ford økte lønningene til 5 dollar dagen, noe som var mye høyere enn vanlig lønn på det tidspunktet.

Ideen er at hvis det er vanskelig å oppdage innsats på jobben så har arbeidstakere en insentiv til å skulke og ikke jobbe hardt. Hvis de får markedslønn og blir tatt, så er det ikke farlig siden de kan finne en lignende jobb med lignende lønn en annen plass.

Men hvis man tilbyr høyere lønn, så er kostnaden av å miste jobben mye høyere, så man har en insentiv til å jobbe hardt så at man beholder jobben.

Med andre ord, med høy lønn så har man også mer å tape.

Oppsummering: Effektivitetslønn

• Arbeidsgivere har en insentiv å gi en høyere lønn enn nødvendig for å beholde de beste arbeidere.
• Særlig når det er vanskelig å måle innsats på jobben

Minste lønn

Lover som etablerer minste lønn kan også føre til høy strukturelle ledighet.

Vi kan tenke på arbeidskraft som andre markeder: noe med tilbud og etterspørsel.

I grafen viser en etterspørselskurve og tilburdskurve for arbeidskraft.

Markedslønn, \(w*\), er stedet der disse kurvene treffer hverandre

Den vannrette linjen representerer en minstelønn. Minstelønn loven gjør det sånn at tilbud av arbeidskraft øker til N, men at etterspørsel går ned til L_A. Arbeidsledighet blir da forskjellen mellom N og L-A

• w: reallønn
• w*: markedslønn
• w-min: minimumslønn
• Lᴬ: Etterspørsel etter arbeidskraft
• N: Tilbud på arbeidskraft
• Arbeidsledighet: u = N - Lᴬ

Øvelse

Minstelønn regler kan ha effekten av å svekke en økonomiens evne til å tilpasse seg. La oss si at økonomien opplever økt automatisering. Hvordan vil det påvirke vår tilbud og etterspørsel av arbeidskraft? Hvis vi har en konstant minstelønn, hvordan ville det påvirke arbeidsledighet.

Vis svar

Inntektskampsmodellen

Inntektskampmodellen skal modellere forholdet mellom arbeidsmarkedet og priser, og vi vil bruke den til å beskrive hvordan vi tenker på inflasjon som noe som kommer hovedsakelig fra forholdene i arbeidsmarkedet.

En viktig antakelse i modellen: Den grunnleggende årsaken til arbeidsledighet er markedsmakt.

Vi begynner med noen variabel-definisjoner:

• W = lønnsnivå
• w = reallønnsnivå (W/P)
• u = ledighetsraten
• L = Sysselsetting

Vi skal også benytte oss av en produktfunksjon som er så enkel som mulig:

$$Y=AL$$

Hvor A er Totalfaktorproduktivitet / Arbeidsproduktivitet (A = Y/L). Legg merke til at vi har ingen K i denne produktfunksjonen. Vi ser på arbeidskraft som eneste innsatsfaktor.

Vi kan regne ut arbeidskostnader per produsert enhet

$$\frac{wL}{Y} = \frac{wL}{AL} = \frac{w}{A}$$

Prissetting

Nå kan vi lage en enkel modell for hvordan vi tenker en bedrift vill sette sine priser:

$$P = \frac{(1+m)W}{A}$$

Her sier vi at vi skal sette våre priser til å være likt vår enhetskostnad (W/A) der vi også skal sette på et prispåslag (1+m). Dette prispåslaget er basert på hvor mye markedsmakt det er i økonomien.

Vi kan skrive om hvor ligning så at reallønn er venstre side:

$$w=\frac{W}{P} = \frac{A}{1+m}$$

I en figur med reallønn (w) på y-aksen og arbeidsledighet på x-aksen, så kan vi tegne inn dette som en vannrett linje (uavhengige av arbeidsledighet)

Lønnsdannelse

Nå har vi sett prissetting fra bedriftens perspektiv. Nå skal vi se litt på prosessen for å sette lønn fra arbeidstakerens perspektiv.

Vi modellere lønnsetting som en maktspill mellom arbeidstakere og arbeidsgivere (dette er hvor kampen i inntektskampmodellen kommer fra.)

Vi skriver at nominell lønn kan bestemmes av:

$$W = \frac{fA^eP^e}{u}$$

Der

• u: arbeidsledighet
• \(P^e\): Forventet prisnivå
• \(A^e\): Forventet produktivitet
• \(f\): Lønnspressfaktor (rest-post)

Først, merker vi at lønnsforhandlingene er opptatt av framtiden. Arbeidstakeren skal forhandle basert på forventet prisnivå for den kommende perioden og forventet produktivitet. Hvis prisnivå er forventet å øke, så vil arbeidstakerene forhandle å få høyere kompenserende lønn.

Også hvis arbeidstakerene kan overbevise at de vil bli mer produktiv, \(A^e\), i perioden som kommer, så vil de også kreve høyere lønn.

Arbeidsledighet blir en viktig faktor i denne modellen. Tanken er at hvis det er høy arbeidsledighet så vill forhandlingsmakten til arbeidstakerene være svekket. En arbeidstaker som krever høyere lønn kan bli erstattet av en av de mange arbeidsledige.

Det siste elementet er det vi kaller lønnspressfaktoren, f.

Lønnspressfaktoren er best sett som en type respost der man setter alt annet som kan påvirke forhandlingene om lønn. Alle disse faktorene er satt inn på en måte så at de øker lønnet.

Ofte er f tolket som strukturelle faktorer i en økonomi som kan påvirke lønnsnivå. For eksempel:

• Fagforeningsmakt: er det en økonomi med høy andel arbeidstakere som er organisert i fagforeninger, og har disse fagforeningene mye makt. Frankrike ville, for eksempel, vært et land med sterke fagforeninger, mens USA har relativt svake fagforeninger.
• Arbeidsledighetenstrygd - hvis et land har høy og sjenerøs arbeidsledighetnstrygd, så vil arbeidstakerene ha mer forhandlingsmakt, siden alternativet til å jobbe er forholdsvis godt betalt arbeidsledighetstrygd.
• Jobb-beskyttelse. Hvis det er vanskelig å sparke en arbeider, så har også arbeidstakere mer makt i forhandlingene.

Vi skal også tenke at arbeidstakerene er opptatt av reallønn - hvor mye de kan egentlig kjøpe med sitt lønn, så vi skriver om vår ligning som:

$$\frac{W}{P} = w = \frac{fA^eP^e}{uP}$$

Likevekt i inntektskampmodellen

Nå kan vi tegne inn vår lønnsdannelse kurv i samme figur med vår prissettingsregel.

Vi ser at vi får en likevekt der vår arbeidsledighet er bestemt.

Så i denne modellen, så har vi en prissettings regel som er basert på en enkel produktfunksjon og vi har en regel for lønnsdannelse basert på forventninger om prisnivå og produktivitet. Disse sammen bestemmer hvor mange som er arbeidsledige.

Algebraisk likevekt

Algebraisk, så kan vi beskrive vår likevekt ved å sette sammen vår prissetting og lønnsdannelse ligninger:

$$w=\frac{A}{1+m}$$ $$w=\frac{fA^eP^e}{uP}$$ $$u\frac{A}{1+m} = \frac{fA^eP^e}{P}$$ $$u^* = \frac{fA^eP^e}{P}\frac{1+m}{A}$$

Men vi kan også se at vi får en forenklet ligning hvis vi antar at våre forventninger er korrrekte: \(A=A^e\) og \(P=P^e\):

$$\bar{u} = (1+m)f$$

I dette tilfellet er arbeidsledighet basert bare på to ledd: markedsmakt i økonomien (m) og de strukturelle faktorene i f.

Vi kan tolke \(\bar{u}\) som den langsiktige strukturelle ledighetsraten basert på strukturelle faktorer i økonomien.

Men ledighetsraten kan avvike fra det nivået på kort sikt på grunn av avvik i forventninger i prisnivå og produktivitet!

Eksempel: Uforventet prisvekst

La oss si at en økonomi opplever (realisert) prisvekst i løpet av et år. I følge inntektskampmodellen hvordan vil dette påvirke inntektskampmodellen? Vis i en figur.

Eksempel: Økt konsentrasjon i industri

De siste årene så har det vært en trend mot økt konsentrasjon av industri i både USA og Europa. Hvis vi tolker dette som økt markedsmakt i en økonomi, hvordan vil dette påvirke arbeidsledighet i likevekt i vår inntektskampmodell?

Øvelser

Teknologi og inntektskampmodellen

Når datamaskinen ble introdusert i arbeidsplassen, hvilken effekt hadde dette på arbeidsledighet i følge inntektskampsmodellen? Gå ut i fra at arbeidsledigheten er i utgangspunkt på sitt langsiktig, strukturelle nivå. Vis i figuren. Forklar intuisjonen.

Vis svar

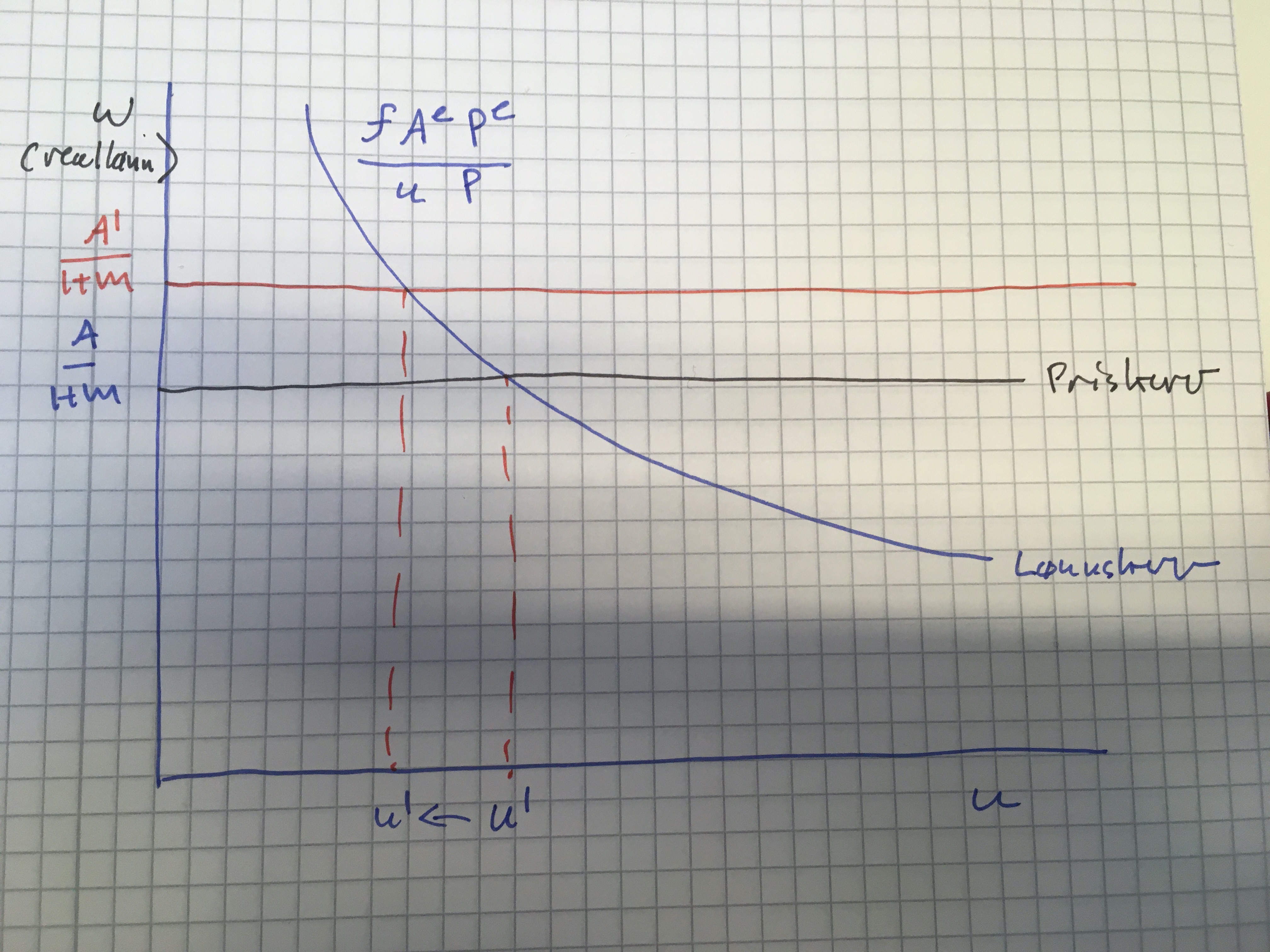
Realisert prisvekst i løpet av et år viser seg til å være høyere enn forventet. Hvordan påvirker dette arbeidsledighet i inntektskampmodellen. Vis i figuren, forklar.

Vis svar

Phillipskurve: Forholdet mellom inflasjon og arbeidsledighet

På 1950 tallet var det en samfunnsøkonom fra New Zealand som het William Phillips. Phillips hadde sammenlignet data om inflasjon og arbeidsledighet over tid i en rekke land, og han oppdaget at han kunne tegne en kurv som slakte nedover med inflasjon på y-aksen og arbeidsledighet på x-aksen. Dette ble kalt "phillipskurven", men det var på den tiden bare en empirisk observasjon. Vi har nå de teoretiske verktøyene å forstå hvorfor forholdet mellom inflasjon og arbeidsledighet oppstår, og også hvordan den bryter ned.

Vi har etablert en modell som kobler sammen arbeidsmarkedet og ledighet med prissetting, så nå kan vi fortsette med å analysere forholdet mellom inflasjon (økning i prisnivået) og arbeidsledighet.

Vi begynner med vår likevekt fra inntektskampmodellen:

$$u = (1+m)f \frac{P^e}{P}\frac{A^e}{A}$$

Vi definerer inflasjon, \(\pi\) som:

$$\pi = \frac{P-P_0}{P_0} =\frac{P}{P_0}-1$$ $$\frac{P}{P_0} = 1+\pi$$ $$\frac{P/P_0=1+\pi}{P^e/P_0 = 1+\pi^e}$$ $$\frac{P}{P^e} = \frac{1+\pi}{1+\pi^e}$$

Hvis vi nå går tilbake til vår likevekt i inntektskampmodellen:

$$u = (1+m)f \frac{P^e}{P}\frac{A^e}{A}$$

Og vi husker at vi definerer den langsiktig strukturelle arbeidsledigheten som når \(P=P^e\) og \(A=A^e\)

$$\bar{u}=(1+m)f$$

Vi kan da skrive:

$$\frac{\bar{u}}{u} = \frac{(1+m)f}{(1+m)f\frac{P^e}{P}\frac{A^e}{A}}$$

Vi er hovedsakelig interessert i effekten av pris her, så la oss holde \(A^e=A\). Da får vi:

$$\frac{\bar{u}}{u} = \frac{P}{P^e} = \frac{1+\pi}{1+\pi^e}$$ $$1+\pi = (1+\pi^e) \frac{\bar{u}}{u}$$

Figuren under viser dette forholdet.

Øk u Reduser u

Figuren viser at på kort sikt så kan vi oppleve en avveining mellom inflasjon og arbeidsledighet. Vi kan få arbeidsledighet til å senke på kort sikt ved å akseptere litt høyere inflasjon.

Men legg merke at dette bare fungerer så lenge realisert inflasjon viker fra forventet inflasjon.

Langsiktig arbeidsledighet er basert på strukturelle faktorer og er ikke relatert til inflasjon - derfor viser vi en loddrett linje som representerer den "langsiktig phillipskurv" - der det er ingen avveining mellom inflasjon og arbeidsledighet.

Pengepolitikk, den nøytrale renten og phillipskurven

Produksjonsgap og den nøytrale renten

Vi skal nå tilbake til vår diskusjon om pengepolitikk, og se hvordan vi kan koble sammen pengepolitikk med vår forståelse av inflasjon.

Vi husker begrepet av normalt-BNP (eller potensielt BNP), som vi skal skrive som \(\bar{Y}\).

Forskjellen mellom virkelig BNP og normalt-BNP skal vi kalle produksjonsgapet, x, som vi skriver som en brøkdel.

$$y_{gap}=\frac{Y-\bar{Y}}{\bar{Y}}$$

Hvis vi husker at den nøytrale renten, \(\bar{r}\), er renten som fører til at BNP når sit normalt nivå, så kan vi beskrive normalt BNP i en lukket økonomi som:

$$\bar{Y} = \frac{1}{1-c}[G+b+I_0 - v\bar{r}]$$ $$\bar{Y} = \frac{1}{1-c}[G+b+I_0]- \frac{v}{1-c} \bar{r}$$

Hvis vi vil regne ut den absolutte produksjonsgapet, \(Y-\bar{Y}\) så kan vi da regne ut:

$$Y = \frac{1}{1-c}[G+b+I_0] - \frac{v}{1-c}r$$ $$\bar{Y} = \frac{1}{1-c}[G+b+I_0]- \frac{v}{1-c} \bar{r} $$

Og dermed:

$$Y-\bar{Y} = \frac{-v}{1-c}[r-\bar{r}] = z[r-\bar{r}]$$

der \(z=\frac{-v}{1-c}\)

Fra denne ligningen kan vi se at produksjonsgapet er proporsjonalt med forskjellen mellom renten og den nøytrale renten.

Produksjonsgapet, phillipskurven og forventet inflasjon

Tidligere i forelesningen, så hadde vi et forhold basert på inntektskamp-modellen som sa at inflasjon var en funksjon av forventet inflasjon, og forskjellen mellom den strukturelle og faktiske arbeidsledighetsraten.

Nå bruker vi begrepet produksjonsgap til å erstatte arbeidsledighetsraten (høy kortsiktig arbeidsledighet er tegn på produksjonsgap.)

$$\pi = \pi^e + \alpha [y_{gap}] + k$$

Der vi tolker k som en kostnadssjokk

Nå kan vi tegne inn dette forholdet

Øk Y-gap Reduser Y-gap Øk forventet inflasjon

I denne kurven kan vi se at på kort sikt så varierer vår inflasjon med produksjonsgapet, gitt en fast forventet inflasjon. Hvis du trykker på knappen Øk forventet inflasjon, så ser du at hele kurven hopper opp til et nytt nivå.

Vi kan også se på den langsiktig phillipskurven som er en loddrett linje der produksjonsgapet er null. På langsikt, der produksjon er likt sin normalt-nivå, så er det ingen sammenheng med inflasjon og

Kanskje det viktigste å se her er hvor viktig forventninger spiller inn. Og det blir også viktig når vi skal analysere pengepolitikk fra sentralbanken.

Litt senere i kurset, kommer vi til å se mer i detalj på ideen om inflasjonsstyring. Men ideen er at en sentralbank med troverdig pengepolitikk skal kunne klare å skape forventninger om inflasjon. For eksempel, Norges Bank har et inflasjonsmål på 2%. Inflasjonsmålet er sentralbankens måte å prøve å påvirke forventninger.

Hvis vi har en sentralbank med troverdig inflasjonsmål, \(\bar{\pi}\), så kan vi skrive:

$$\pi = \bar{\pi} + ay_{gap} + k$$

Så nå kan vi skape et sammenheng mellom avvik fra inflasjonsmålet og avvik fra den neutrale renten:

$$\pi - \bar{\pi} = a[y_gap] + k$$ $$y_{gap} = \frac{Y-\bar{Y}}{\bar{Y}} = \frac{\frac{-v}{1-c}(r-\bar{r})}{\bar{Y}}$$ $$\pi - \bar{\pi} = \frac{-av}{(1-c)\bar{Y}}(r-\bar{r}) $$ $$\pi - \bar{\pi} = -az(r-\bar{r}), z=\frac{v}{(1-c)\bar{Y}} $$

Der vi kaller \(\pi - \bar{\pi}\) inflasjonsgapet.

Taylorsregelen for pengepolitikk

Økonomenen John Taylor så på amerikanske rentesetting, og formulerte følgende ligning for observert rentesetting.

$$i = \pi + \tilde{r} + d_1(\pi - \bar{\pi}) + d_2 y_{gap}$$

Eller

$$r= i-\pi = \tilde{r} + d_1(\pi - \bar{\pi}) + d_2x y_{gap}$$

der \(\tilde{r}\) er en en konstante, langsiktige likevektsrente (hvordan er dette annerledes enn neutrale renten? Nominelle renten er en kombinasjon av inflasjon, langsiktige realrenten, inflasjonsgap og produksjonsgap.

Inflasjon i en åpen økonomi

I en åpen økonomi, er inflasjon påvirket av prisene på import varer.

$$P = KPI \approx (EP^*)^p(P_H)^{1-p} = (EP^*)^p(P_H)^1(P_H)^{-p} = (\frac{EP^*}{P_H})^p P_H$$

\(P_H\): prisnivå av varer og tjenester produsert i hjemlandet

p = andel varer vi importerer.

Hvis vi setter P=KPI

Og bruker defn på realvalutakurs

$$\epsilon = \frac{EP^*}{P} \approx \frac{EP^*}{KPI} = \frac{EP^*}{(\frac{EP^*}{P_H})^p P_H} = (\frac{EP^*}{P_H})^{1-p} => \frac{EP^*}{P_H} = \epsilon^{\frac{1}{1-p}}$$

Det vil si at det er et forhold mellom prisene i utlandet og prisene i hjemlandet.

Tilbake til vår defn av KPI

$$KPI= (\frac{EP^*}{P_H})^p P_H$$

KPI (prisnivået går opp hvis kronen svekker seg (realdepresieres) I vekst format:

$$\pi_{KPI} = \frac{p}{1-p}g_{\epsilon} + \pi_H$$

Inflasjon i vår økonomi kommer fra to plasser, hjemmeprodusert varer og tjenester, og realvalutakurset (vektet med andel varer som vi importerer)

Hvis vi ser på inflasjonsgapet:

$$\pi_{KPI} - \bar{\pi} \approx \frac{p}{1-p}g_{\epsilon} + (\pi_{H}-\bar{\pi})$$

vekst i realvalutakursen (realdepresiering) bidrar positivt til inflasjonsgapet i en åpen økonomi.

Innenlandsk inflasjon kan vi beskrive som fra i går:

$$\pi_H - \bar{\pi} = ay_{gap} + k$$

Og vi husker at vi kan skrive produksjonsgapet som en funksjon av avvik neutrale renten:

$$y_{gap} = \tilde{z}(\bar{r}-r)$$

vi brukte vanlig z før, nå med tilde bare for å skille at nå snakker vi kun om hjemmemarkedet.

så kan vi skrive

$$\pi_{KPI} - \bar{\pi} \approx \frac{p}{1-p}g_{\epsilon} + (\pi_{H}-\bar{\pi})$$ $$\pi_{KPI} - \bar{\pi} \approx \frac{p}{1-p}g_{\epsilon} + a\tilde{z}(\bar{r}-r) + k$$

Inflasjonsgapet kommer fra avvik fra neutrale renten, endring i importpriser, og kostnadssjokk.